
Nous avons vu dans notre dernier article que les grands principes de fonctionnement de l’apprentissage par renforcement illustrés par un cas pratique autour de l’exemple du Cart-Pole d’OpenIA.
Plus particulièrement, dans cet article, nous allons voir comment l’expérience utilisateur (UX design) sur un site web peut être optimisée par des techniques de renforcement learning (RL). En effet, le machine learning rend de plus en plus possible la personnalisation des contenus web et des parcours client.
Qu’est-ce exactement que l’optimisation de l’expérience utilisateur (UX design) ?
L’expérience utilisateur (User eXperience ou UX en anglais) permet de qualifier le ressenti d’un utilisateur face à une plateforme (écran tactile, pupitre opérateur, site web, …) en prenant en compte les résultats de cette expérience. Ainsi, la terminologie UX englobe toutes les techniques permettant d’améliorer l’expérience d’un utilisateur sur une plateforme.
Dans cet article, nous allons focaliser nos propos sur l’UX design appliqué au web. Il s’agit de l’expérience utilisateur qui permet de créer pour l’internaute une véritable expérience lors de sa visite sur un site internet. L’objectif est de proposer un parcours client clair (ergonomie réussie), simple à prendre en main, agréable, fluide (recherche optimale des informations), efficace (navigation optimisée et, idéalement responsible design sur mobile ou tablette) et centré sur le seul ressenti de l’utilisateur. L’expérience utilisateur est donc une priorité dès la création d’un site internet.
Notre algorithme de renforcement learning (notre IA) va permettre :
- De maximiser la probabilité de transformation et donc de passage à l’acte commercial pour un maximum de clients (achats, ajout d’un produit dans le panier web, …)
- D’obtenir de meilleures performances par rapport aux méthode d’A/B testing.
Techniquement, l’UX design vu au travers du prisme de l’apprentissage par renforcement (RL), c’est, par exemple :
- Proposer un design, puis un autre design en fonction des retours d’« expériences » des utilisateurs (agents) : il s’agit de l’action.
- Analyser la conversion du client (achat ou non) en fonction des différents designs proposés : il s’agit de la récompense associée à l’action.
Dans cet exemple, l’objectif des designers consiste à trouver de façon itérative le meilleur design, c’est-à-dire celui qui maximise les récompenses.
L’algorithme du bandit manchot
En réalité, ce problème est bien connu dans le domaine de l’apprentissage par renforcement. Il s’agit du problème dit du bandit manchot (en anglais, « Multi Armed Bandit »). Dans notre exemple précédent autour de l’optimisation du design d’un site web, on peut formuler ainsi notre problème du bandit manchot : un utilisateur est face à notre site web et il réalise ou non un ensemble d’actions (achat en ligne, produit mis au panier, …). Cela attribue à notre design un score moyen de récompense. In fine, c’est le design qui maximise les récompenses qui est retenu.
Dans la suite de notre article, nous allons présenter deux algorithmes du bandit manchot :
- « Upper Confidence Bound (UCB) »
- « Lower Upper Confidence Bound (LUCB) »
Dans un premier temps, nous allons rappeler en quoi consiste l’A/B testing et montrer comment le RL permet de booster les résultats (UCB ou LUCB versus A/B testing traditionnel).
Rappel : quel est le principe de fonctionnement des méthodes d’A/B testing classiques ?
L’A/B test signifie tester une version A versus une version B, comme la terminologie l’indique. Dans notre cas de figure, il s’agit d’une méthode permettant de tester deux versions différentes d’un même site web (design différent pour chaque version).
Le but final est ensuite d’estimer si le design de la version du site web B offre de meilleures performances en termes d’expérience utilisateurs que le design de la version du site B.
Nous pouvons par exemple considérer le nombre moyen de visites web pour chacune des deux versions.
La version du site qui maximise le nombre moyen de visites web étant alors retenue comme la meilleure version du site web.
Figure 1 : Illustration du A/B Testing
Il y a de nombreuses limites pour la mise en œuvre de cette approche :
- D’abord, le résultat dépend fortement de la métrique de performance retenue.
- La comparaison des résultats entre le groupe A et B doit être statistiquement significatif. Or, dans de nombreux cas de figure, le panel de retours utilisateurs est trop faible pour conclure à des résultats fiables. (Il n’y a pas assez d’individus dans nos échantillons A et B pour valider les résultats).
- Une contrainte opérationnelle existe. En effet, si la version B est un échec alors, il y a fort à parier que durant la phase d’A/B test, nous ayons généré un grand nombre d’insatisfaction chez les utilisateurs. En conséquence de quoi, en retour de cette phase d’A/B test, il y a fort à parier que nous perdrons des utilisateurs potentiels.
- Donc l’A/B test peut, dans la pratique, fortement dégrader les ventes et dégrader l’expérience de l’acheteur sur le site web.
Apprentissage par renforcement : UCB ou LUCB ?
Etant données ces limitations et compte tenu de l’avancée des recherches en mathématiques appliquées, d’autres méthodes plus performantes existent.
Dans notre exemple, ces méthodes optimisent le compromis entre : tester de nombreux designs pour notre site web (afin d’en trouver le meilleur) versus ne pas prendre le risque de perdre des clients à cause d’un mauvais design. C’est d’ailleurs, comme expliqué précédemment, l’objectif même du domaine de l’apprentissage par renforcement que de résoudre ce compromis.
Upper Confidence Bound (UCB) ?
Cet algorithme est souvent considéré comme incarnant « l’optimisme face à l’incertitude ». En effet, la fonction de récompense lié au choix de chaque agent (on utilise le terme de « bras ») est estimée à chaque instant dans un intervalle de confiance (intervalle admis d’erreurs sur les résultats).
L’algorithme UCB est optimiste parce qu’il ne va se préoccuper que de la limite supérieure de l’intervalle de confiance et chercher à maximiser les récompenses de chaque agent.
L’objectif principal de cet algorithme : optimiser le rendement moyen au fur et à mesure des itérations, en choisissant les bras les plus prometteurs mais aussi en essayant les bras à qui on n’a pas encore donné une chance.
Il existe différentes variantes de l’algorithme UCB, mais dans cet article, nous allons nous intéresser uniquement à l’algorithme UCB1.
Au cours de la t-ième itération, la borne supérieure de la récompense UCB du bras “i” est représentée par ce qui suit :
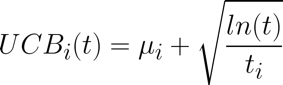
Figure 2 : Borne supérieure du bras i à l’itération t
où :
- µi : représente la moyenne de retour de récompense actuelle du bras i
- t : représente le nombre d’essais global effectué (nombre d’itérations)
- ti : représente le nombre de tirages du bras i
A chaque itération, le bras ayant le terme le plus grand sera tiré.
Le calcul UCB ci-dessus donne une formulation du principe d’augmentation des chances de tirages pour les bras, selon l’ajustement judicieux entre l’exploitation (l’utilisation systématique des versions du site web à l’origine de nombreuses récompenses) et l’exploration (tester des nouveaux design de site web pour espérer gagner plus que pour les version de site connus).
C’est notamment le logarithme “ln(t)” qui permet d’améliorer le compromis entre l’exploration et l’exploitation au fil des itérations.
Learning by doing : exemple de script Python
La fonction principale Pull de cet algorithme permet de retenir le bras avec la plus grande expression formulée (formule ci-dessous).
Cette fonction permet également la mise à jour de l’estimation de la récompense de ce bras et de la borne supérieure de son intervalle de confiance.
|
def pull(self):
# Update reward and counts # Update mean rewards # Update reward for the selected arm |
Voici l’évolution des récompenses totales, itérations après itérations (cas d’une seule simulation avec 10 bras, 10 récompenses tirées suivant la loi normale N(0, 1), 100 itérations au total).
Dans notre exemple basé sur une unique simulation, on constate une nette amélioration des récompenses au fil des itérations, jusqu’à l’obtention d’un régime permanent constant (en moyenne).
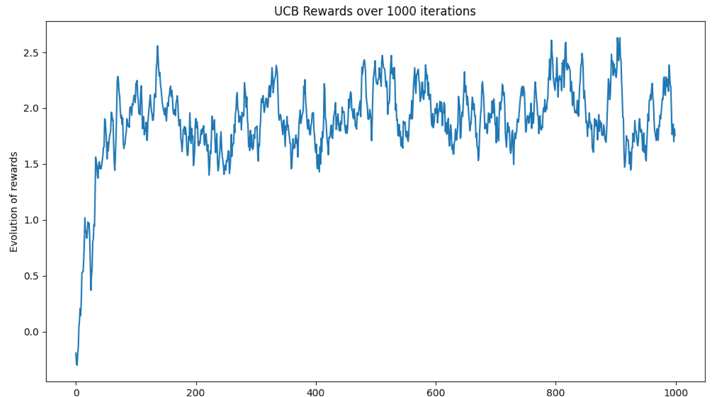
Figure 3 : Evolution de la moyenne des récompenses au fil des itérations
A noter qu’il aurait été pertinent d’effectuer un grand nombre de simulations, de les moyenner afin de liser la courbe de résultats pour accentuer nos résultats.
Lower Upper Confidence Bound (LUCB) ?
Cet algorithme a pour point commun avec l’UCB qu’il est également basé sur la mesure de l’intervalle de confiance de l’estimation des récompenses de chaque bras à chaque itération.
Par contre, cet algorithme se concentre à la fois sur la borne supérieure et sur la borne inférieure de l’intervalle de confiance.
L’objectif principal de cet algorithme : trouver les K meilleures bras parmi N bras, tel que K < N.
Dans notre cas de figure, il existe différentes variantes de l’algorithme LUCB. Nous allons nous intéresser exclusivement à l’algorithme LUCB1.
L’idée principale de l’algorithme est de répartir à chaque itération les bras en deux groupes :
- Groupe TOP qui contient les K bras avec les plus grandes estimations µi
- Groupe BOTTOM qui contient les N-K bras avec les plus petites estimations µi
Ensuite, afin d’effectuer le tirage, l’algorithme choisit entre deux éléments :
- l’élément de TOP ayant la plus petite borne inférieure, nommé Lcb_arm
- l’élément de BOTTOM ayant la plus grande borne supérieure, nommé Ucb_arm
L’algorithme met en concurrence les deux bras en considérant que statistiquement, il existe une chance (probabilité favorable) pour que l’Ucb_arm (du groupe BOTTOM) soit meilleure que Lcb_arm (du groupe TOP).
L’algorithme s’arrête à l’itération où tous les éléments appartenant à TOP sont significativement plus performants que tous les éléments de BOTTOM (à un epsilon près traduisant une marge d’erreurs possible).
A noter qu’au fur et à mesure des itérations, les bras changent de groupe puisque les estimations µi sont mises à jour à chaque itération.
Prenons un exemple afin d’illustrer ce fonctionnement. Soit 5 bras notés “a”, “b”, “c”, “d” et “e” dans la disposition suivante, à une itération donnée t.
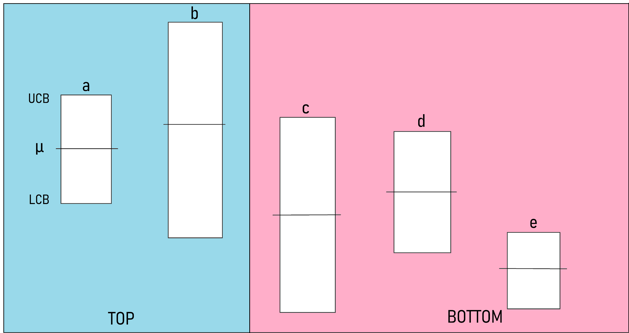
Figure 4 : Simulation avec 5 bras
On constate que :
- Les µi de BOTTOM = (c, d, e) sont plus petites que les µi des bras de TOP = (a, b)
- Le bras ayant la plus petite borne inférieure dans TOP est le bras b, nommé Lcb_arm
- Le bras ayant la plus grande borne supérieure dans BOTTOM est c, nommé Ucb_arm
- Les deux bras qui seront donc mis en concurrence sont b et c (afin de vérifier que b a bien sa place dans le groupe TOP).
La formule de LUCB des intervalles de confiance est faite de manière à privilégier les bras qui n’ont pas été tirés (exploitation) tout en gardant les chances des bras déjà performants (exploration).
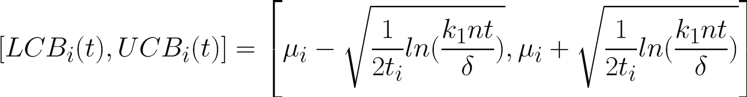
Figure 5 : Intervalle de confiance du bras i à l’itération t
avec :
- k1 : une constante ici égale à 5/4
- n : le nombre total de bras
- t : une itération donnée
- ti : le nombre de tirage du bras i
- delta : un paramètre entre 0 et 1 à fixer lors de l’initialisation
Pour ceux qui souhaitent approfondir du point de vue théorique les notions de UCB & LUCB, je vous invite à lire cet article et notamment la partie 3 “LUCB”, le théorème 1 dans la partie 3 et le lemme 3.3.
Attention : dans l’article, certaines variables ont des noms différents.
Le critère d’arrêt de l’algorithme correspond au moment où la différence entre la borne inférieure de Lcb_arm et la borne supérieure de Ucb_arm est inférieure à un ε à définir au début du lancement.
Learning by doing : exemple de script Python
Dans cette simulation, nous allons considérer que les retours peuvent être 0 ou 1.
La fonction principale permettant d’effectuer les tirages et d’effectuer la mise à jour des différents paramètres est, à nouveau, nommée Pull.
Conformément aux explications données ci-dessus, cette fonction permettra :
étape 1 – d’ordonner les bras suivant l’estimation de leurs récompenses à l’instant t
étape 2 – de diviser les bras en deux groupes : K bras dans TOP et N-K bras dans BOTTOM
étape 3 – de prendre l’élément de TOP avec la plus petite borne inférieure
étape 4 – de prendre l’élément de BOTTOM avec la plus grande borne supérieure
étape 5 – de vérifier si le critère d’arrêt est atteint (si oui on s’arrête, sinon on continue)
étape 6 – de mettre en concurrence les deux éléments de l’étape 3 : elle en choisit un de manière aléatoire
étape 7 – mettre à jour les paramètres
|
def pull(self): # sort arms according to their rewards # divide them in two groups of k and n-k # take arm from top with lowest lcb # if stop criteria met then stop # Select random arm among lcb and ucb arms : # sample reward according to the arm’s real reward # update counts # Update total # Update results for t_i print(« iteration », str(self.t), « diff », abs(lcb_arm[‘lcb_i’] – ucb_arm[‘ucb_i’]), ‘id’, str(a)) |
Dans cet exemple, la configuration de notre simulation est :
- nombre de bras total n = 5
- nombre de bras à retenir k = 2
- delta = 0.1
- epsilon = 0.1
- récompenses respectives = [ 0, 0.25, 0.5, 0.75, 1]
Voici les résultats finaux, en notant que les mu_i sont les estimations trouvées par l’algorithme :

Figure 6 : Résultats de la simulation LUCB
Analyse des résultats de simulation
- L’algorithme a mis 16187 itérations pour s’arrêter : il s’agit du total des ti
- les deux bras d’id 3 et 4 ont les meilleures récompenses (ce qui était prévisible)
- le bras d’id 0 n’a été tiré que 439 fois parmi les 16187, ses retours étant toujours nuls
- le bras d’id 1 n’a été tiré que 1255 fois, plus que le bras 0, mais beaucoup moins que les bras 2 et 3
- les deux bras qui ont été tirés les plus souvent sont les bras 2 et 3 (l’algorithme a su écarter le doute)
- à l’issue de 1158 tirages pour le bras 4, l’algorithme a compris que c’était ce bras 4 qui était le meilleur de tous. L’algorithme a donc ensuite mis en concurrence les bras 2 et 3 pour vite les départager dans la course à la deuxième place du classement.
Tout se déroule comme prévu. LUCB a réussi à retenir les K meilleurs bras parmi N de manière statistiquement correcte, sans trop perdre son temps à essayer des bras nuls comme le bras d’identifiants 0 ou 1 (tout en donnant la chance aux bras qui avaient encore une chance statistiquement d’être parmi les K meilleurs).
Architecture Google Cloud Plateform (GCP) pour mettre en œuvre ces algorithmes
Pour donner les grands principes de l’industrialisation des algorithmes décrits ci-dessus, nous allons mettre en œuvre une architecture avec une base de données relationnelles constituée principalement de :
- Une table pour les designs à tester (designs des différentes versions de sites web)
- Une table pour les envois / retours des expériences utilisateurs
- Une table pour l’évolution des paramètres : intervalles, estimations, probabilités de tirage …
Un petit détail est à noter :
Si au cours d’une itération t, nous voulons que deux bras soient testés, il faut alors mettre une colonne qui indique les bras “disponibles” pour le tirage. Par exemple, pour une simulation de 4 bras avec k égal 2, à une itération t donnée, l’état du système est comme suit :
|
id |
tirable |
|
01 |
0 |
|
02 |
1 |
|
03 |
1 |
|
04 |
0 |
Figure 7 : Exemple de l’état de la table de bras disponibles au tirage
Ainsi, les bras à tester sont les bras 2 et 3. La fonction de tirage s’occupera alors de faire le choix entre les deux bras, de façon complètement aléatoire.
En théorie, les itérations se font de manière incrémentale, mais en pratique, un job va effectuer une mise à jour des variables à des intervalles de temps bien définis (par ex : toutes les 10 min).
Il est indispensable de mettre en place une architecture qui permet à minima d’effectuer ces trois étapes :
- L’enregistrement des retours d’expériences utilisateurs positifs quand l’utilisateur réalise un événement positif (achat, …). Il s’agit des récompenses associées aux pages web
- L’étape de sélection de la page, en fonction des probabilités dans les bases de données à l’instant t
- La réalisation de la mise à jour des différentes variables (par exemple, toutes les 10 minutes)
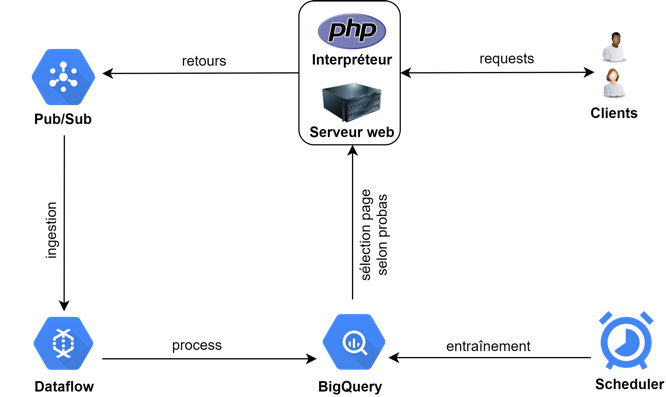
Figure 8 : Schéma de principe d’une architecture GCP
Détails du schéma d’architecture
- Sur ce schéma, l’ensemble Serveur Web / Interpréteur PHP gère les requêtes client / serveur usuelles que nous trouvons sur tous les sites.
- Les retours d’expériences (positifs ou négatifs), sont stockés en flux continu de données. Le service Pub/Sub permet l’ingestion et/ou traitement de flux de données en streaming, découplant les traitements pour permettent une ingestion optimale des données via Dataflow.
- Dataflow procède ensuite au traitement des données pour un stockage dans BigQuery.
- L’ensemble des chaînes de traitement (pipeline) est orchestré via un scheduler qui permet une mise à jour des données, toutes les 10 minutes dans notre exemple. Ceci signifie que notre architecture est quasi temps réel avec ce pas de temps.
Conclusion
Dans cette article assez théorique, nous avons vu un cas d’usage détaillé autour de l’apprentissage par renforcement pour l’optimisation de l’interface de l’utilisateur (UI design web).
Nous avons comparé la méthode classique d’A/B testing avec deux techniques RL avancées, l’UCB et le LUCB.
Nous tenons à préciser que l’architecture GCP donne les grandes lignes du principe de fonctionnement en temps réel pour la mise en œuvre de l’algorithme LUCB.
Dans des cas de mise en œuvre pratique d’architecture GCP, il est bon de noter que d’autres services managés GCP viennent s’ajouter pour :
- Améliorer la sécurisation des rôles/Utilisateur via l’IAM (Identity Acess Management) par exemple
- Pour une mise en œuvre sécurité des pipelines avec, par exemple, l’implémentation de réseaux locaux sécurité VPC (un subnet publique & un subnet privé, …).