
Un algorithme de détection d’anomalies a pour objectif principal de repérer des données atypiques et non conformes aux autres données.
Le problème n’est pas simple parce qu’on ne connaît pas nécessairement au préalable ce qui caractérise une anomalie. C’est alors à l’algorithme d’apprendre une métrique appropriée pour les détecter au sein des données.
Parmi les cas d’usages rencontrés chez nos clients, citons :
- les problématiques de fraudes à la transaction bancaire,
- la détection de défaillances ou d’avaries matérielles dans le cadre de la recherche d’optimisation en la maintenance prédictive.
La détection d’anomalies est généralement une technique d’apprentissage non supervisé qui consiste à détecter dans les données les échantillons dont les caractéristiques sont très éloignées de celles des autres échantillons.
Pour cela, une première approche (théorisée, par exemple, par les méthodes Lean Manufacturing et 6 Sigma), consiste à calculer la moyenne et l’écart-type de nos données pour déterminer une fonction « densité de probabilité ». On utilise ensuite cette fonction pour calculer la probabilité d’existence d’un échantillon atypique de données. La règle est la suivante : lorsque cette probabilité est en dessous d’un certain seuil alors l’échantillon est considéré comme anormal.
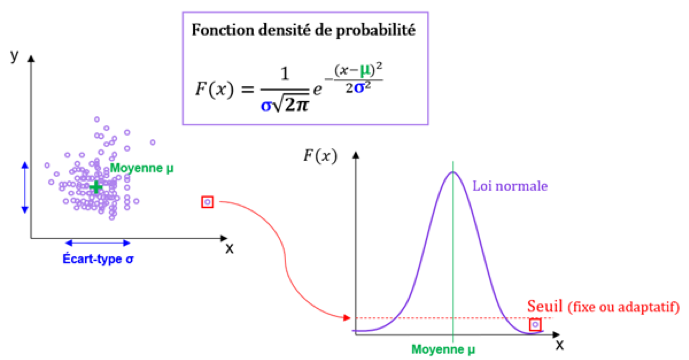
Le seuillage permet d’isoler les anomalies : il peut être fixe ou adaptatif. Dans le cas d’un seuillage adaptatif, le seuil est remis à jour en permanence et s’adapte en temps réel aux données.
Ces techniques sont très efficaces mais depuis quelques années, il existe d’autres méthodes plus modernes pour apprendre à reconnaître des valeurs aberrantes dans les données.
L’isolation forest (moins connu sous son nom français « forêt d’isolement ») calcule un score d’anomalie pour chaque observation du dataset. Ce score donne une mesure de la normalité de chaque observation en fonction de l’ensemble des données. Pour calculer ce score, l’algorithme isole la donnée en question de manière récursive : il choisit une variable au hasard et fixe un seuil de coupure au hasard, puis il évalue si cela permet d’isoler une observation en particulier.
Ce type d’algorithme est à privilégier dans le cas de problèmes mathématiques de grandes dimensions (grand nombre d’observations et de variables).
Fonctionnement illustré
Dans l’exemple qui va suivre, on applique l’isolation forest sur des données contenant deux variables (x et y) et comportant une seule anomalie (le point extrême qui figure en rouge sur le graphique).

Résultat : Voilà, vous avez compris l’idée ! Dans notre exemple, il suffit de seulement 3 splits (on parle aussi de “séparations”) pour isoler l’échantillon en rouge (anomalie supposée du fait de son éloignement aux autres données). Or, dans la masse des données (c’est-à-dire les données “normales”) : il aurait fallu peut-être entre 100 et 400 splits pour isoler un échantillon.
Retenez : plus le nombre de splits est faible et plus la probabilité est forte que l’échantillon observé soit une anomalie.
… Une forêt d’arbre ?
Il est à noter qu’avec le processus de splits aléatoires, il est possible d’isoler à tort un des échantillons de la masse des données (données “normales”). C’est très peu probable mais cela peut arriver. La solution pour palier ce risque d’isoler à tort un échantillon normal consiste à générer plusieurs arbres de décision comme estimateurs. Ces arbres vont chacun effectuer une séquence de splits aléatoires. Ensuite, on va considérer la moyenne de l’ensemble des résultats. On peut ainsi disqualifier les quelques petites erreurs qui peuvent être commises par certains de ces estimateurs parce que la “majorité va l’emporter”. Là encore, les techniques ensemblistes permettent d’apporter une robustesse indispensable à nos résultats.
Mise en œuvre de l’algorithme en Python
C’est la classe sklearn.ensemble.IsolationForest qui permet d’instancier un modèle d’isolation forest.
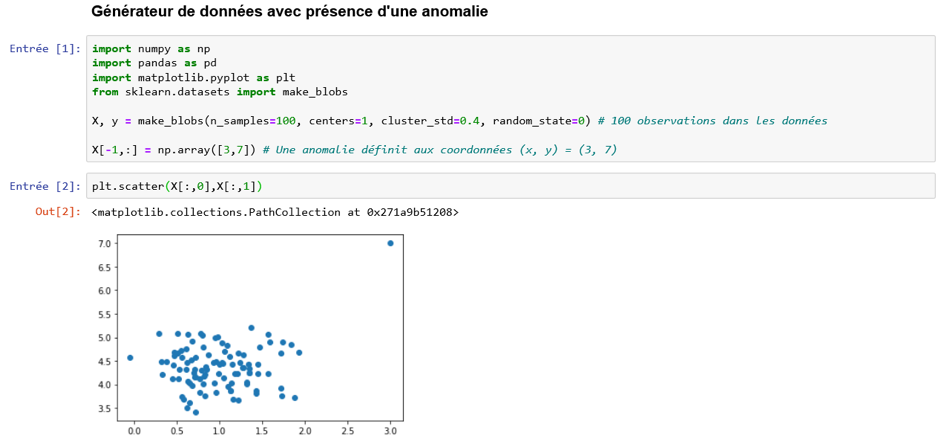
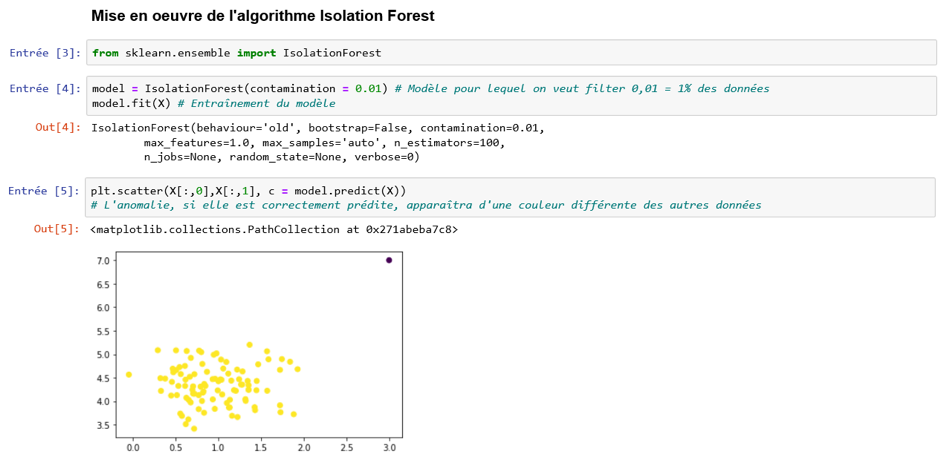
Le résultat est concluant : l’algorithme a bien compris qu’il existe un point aberrant (une anomalie) dans les données.
A noter que dans l’implémentation de sklearn, le seuil des points à considérer comme anormaux est défini par le taux de contamination. Dans notre exemple, le taux de contamination est égal à 0,01 (soit 1%). Ainsi, on considère que nos données contiennent 1% d’anomalies.
Conclusion
Ces trois premiers articles ont été consacrés aux algorithmes à base d’arbres de décisions. Ce sont des algorithmes très utilisés et extrêmement efficaces pour résoudre vos problèmes data.
Si par hasard vous souhaitiez devenir data scientist, alors sachez que vous aurez probablement à décrire le fonctionnement d’un de ces algorithmes lors de vos entretiens de recrutement.