Algorithme N°4 - La régression linéaire pour comprendre les grands principes du Machine Learning

Beaucoup de gens pensent que la régression linéaire est simple : il est simplement question de trouver une droite au milieu d’un nuage de points. Ce n’est pas vrai ! Nous pouvons même dire que la régression linéaire est un modèle faussement simple : vous allez voir pourquoi dans cet article.

Bien modéliser, c’est modéliser un phénomène en trouvant la loi la plus simple possible et la plus facilement interprétable.

A cet égard, cet article présente les étapes théoriques d’un retour d’expérience pour la mise en œuvre d’un modèle linéaire de calcul de durée de vie d’un composant mécanique en vue d’optimiser la maintenance préventive de notre client.

Nous avons pris le parti de conserver une approche statistique mais ne soyez pas effrayés par les formules mathématiques ! Cet article reste destiné au grand public et, nous l’espérions, il sera un bon moyen pour vous de comprendre, dans le détail, quelques fondamentaux du Machine Learning.

Il y a trois étapes clés pour construire le meilleur modèle de régression linéaire :

Commencer par définir une fonction coût : c’est une fonction mathématique qui mesure l’erreur que nous commettons en approximant les données. Nous parlons aussi d’erreur induite par la modélisation,
Minimiser cette fonction coût : il faut trouver les bons paramètres de notre modèle pour minimiser l’erreur de modélisation,
Choisir une méthode de résolution du problème. Il existe deux méthodes :

– une méthode de résolution numérique, la descente de gradient,

– une méthode analytique, la méthode des moindres carrés.

Étape 1 : Construction de la fonction de coût.

Pour construire la fonction de coût, nous devons commencer par définir une fonction hypothèse.

Cette hypothèse se résume ainsi : le modèle dépend d’un ensemble de n variables d’entrée, notées x₁, x₂, … x_n. (Ces variables d’entrée correspondent aux données que nous connaissons. Par exemple, le nombre d’habitants d’une région géographique, le salaire d’un employé ou encore toute autre variable connue).

Ces variables d’entrée vont influencer une variable cible Y inconnue, que nous cherchons à prédire.

Du point de vue mathématique, nous cherchons à déterminer la meilleure fonction hypothèse qui permettra de trouver une relation linéaire approximative entre les variables d’entrée et la variable cible Y.

Pour simplifier l’approche, nous prenons le cas le plus simple de la régression linéaire univariée. Dans ce cas, la régression linéaire s’applique à une seule variable d’entrée et la fonction hypothèse h s’écrit h(X) = a x + b.

Notre problème consiste alors à trouver la meilleure approximation, c’est-à-dire le meilleur couple (a, b) tel que h soit le plus proche possible de l’ensemble des points de nos données. Autrement dit, à partir des données, nous allons apprendre la meilleure relation linéaire qu’il existe entre la valeur d’entrée x et la valeur variable cible Y en entraînant la fonction hypothèse h.

Cette fonction hypothèse est donc une fonction qui modélise l’erreur entre la prédiction du modèle et la réalité des données.

Pour chaque point x, la fonction hypothèse associe une valeur définie par h(x_i) qui est plus ou moins proche de la variable cible y_i. Nous définissons ainsi l’erreur unitaire pour x_i par h(x_i) – y_i. Or, chaque erreur unitaire pouvant être positive ou négative. Ainsi, la somme des erreurs unitaires pourrait se compenser. Il faut donc faire en sorte que la contribution de chaque erreur soit systématiquement pénalisante. Alors, on élève au carré l’erreur unitaire (cf. figure ci-dessous).

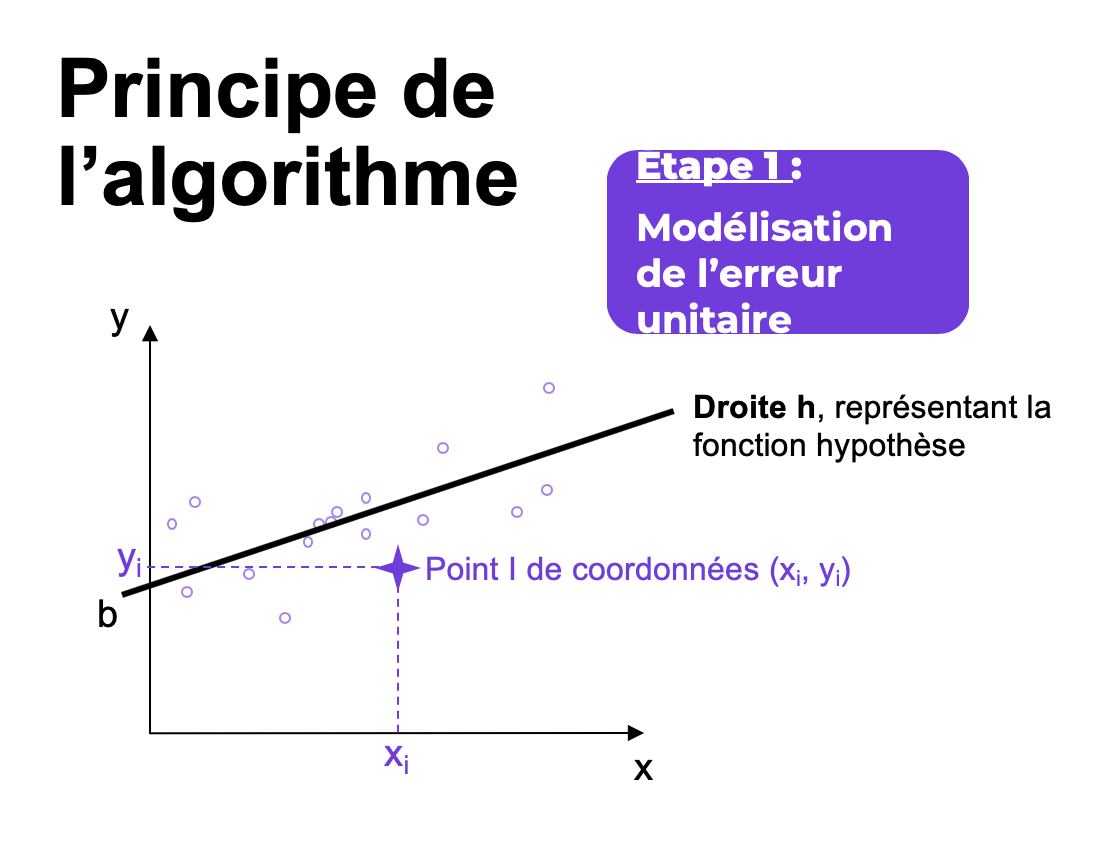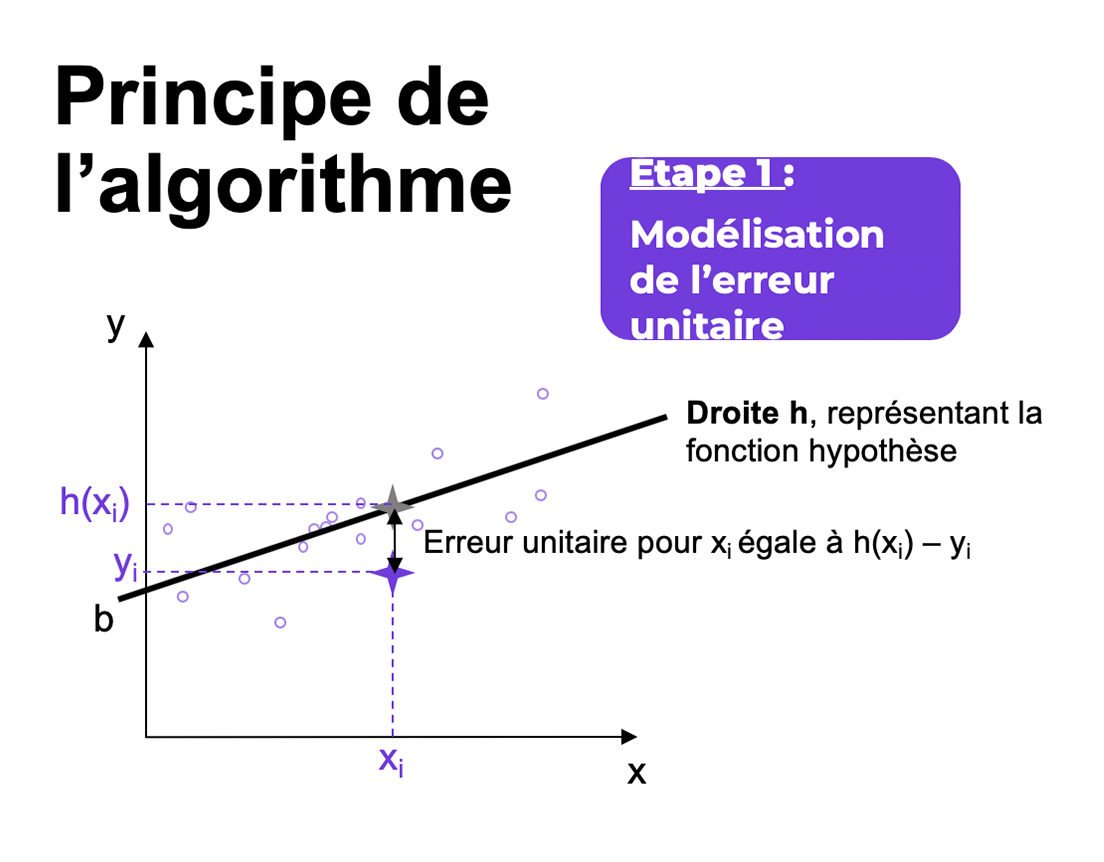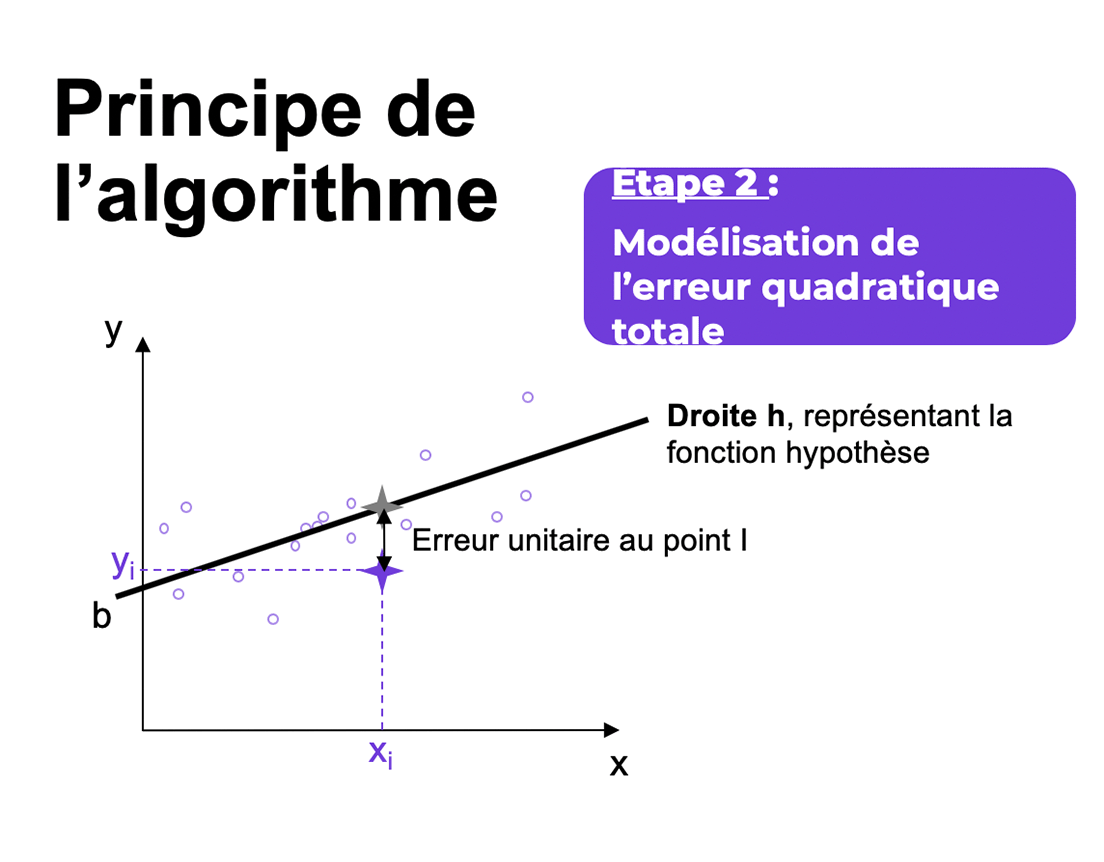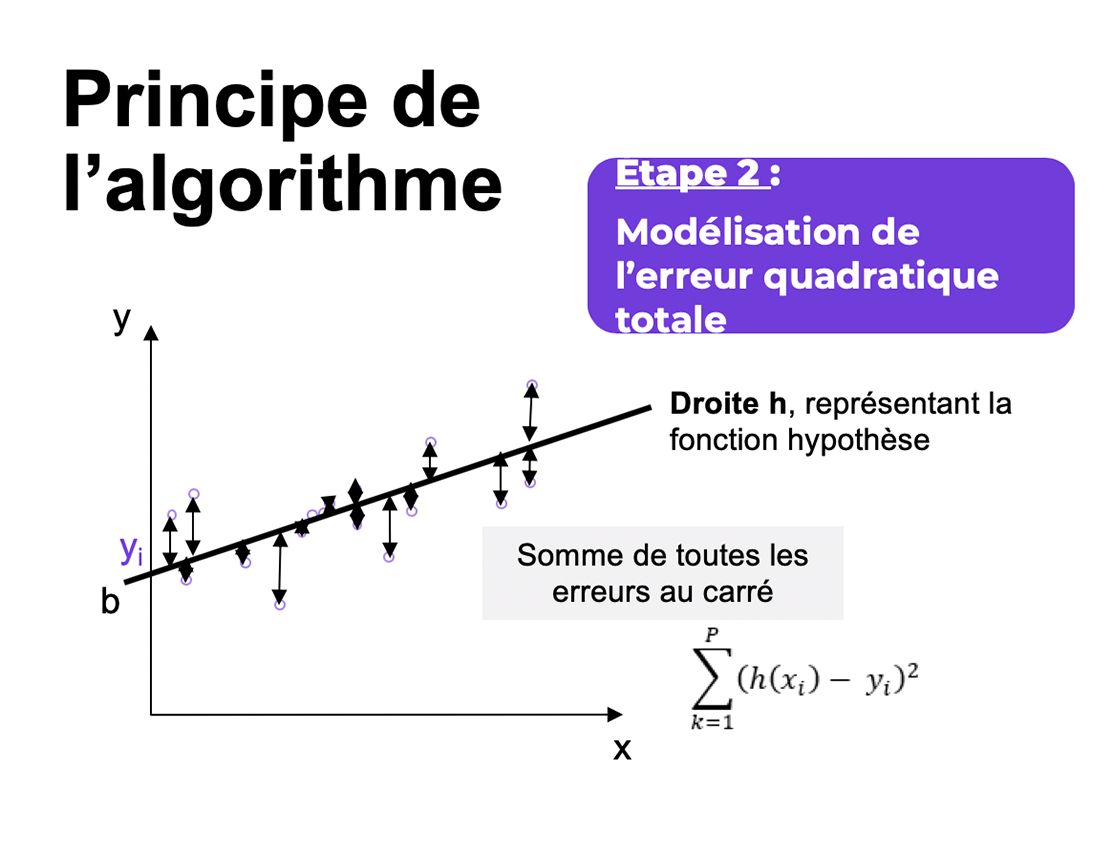
On somme l’ensemble des erreurs unitaires pour l’ensemble des points de données : on parle alors d’erreur quadratique (erreur au carré) :

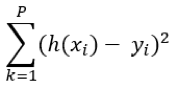
La fonction de coût s’écrit alors en pondérant la somme des erreurs quadratiques par le nombre de points p dans la base d’apprentissage :

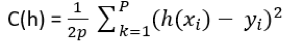
Dans notre cas de régression linéaire univariée, la fonction de coût devient :

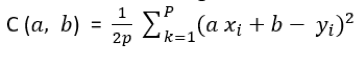
Les valeurs de x et y sont données. La fonction de coût C est, par construction, une fonction des paramètres de la fonction hypothèse h. Et, comme le montre la figure ci-dessus, les paramètres de C définissent une droite affine avec :

b, l’ordonnée à l’origine de la fonction h,
a, le coefficient directeur (ou pente) de la droite h.

Nota : pour la régression linéaire multiple (c’est-à-dire régression linéaire avec n variables d’entrée), c’est le même principe.

Étape 2 : Minimisation de la fonction de coût

Déterminer les meilleurs paramètres (a, b) pour la fonction hypothèse h revient à trouver la meilleure droite, celle qui minimise la somme de toutes les erreurs unitaires.

Du point de vue arithmétique, il s’agit de trouver le minimum de la fonction de coût.

L’opération de mise au carré de la somme des erreurs unitaires permet deux choses :

D’une part, assurer que la fonction de coût est forcément pénalisée par chaque erreur unitaire. En effet, toutes les erreurs sont positives,
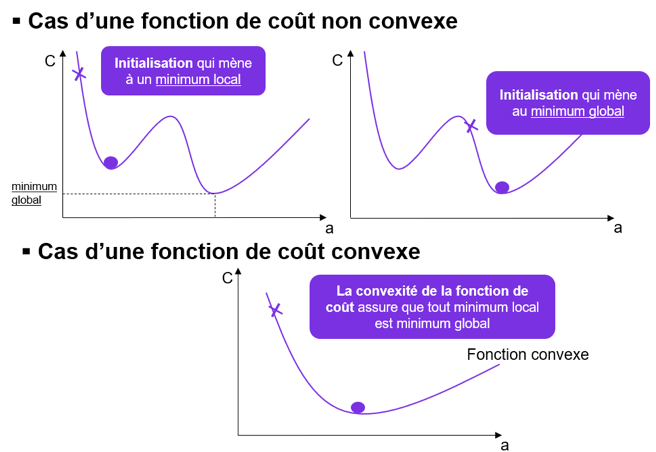
D’autre part, garantir que la fonction de coût est convexe (si la fonction de coût admet un minimum, ce minimum est le minimum global de la fonction). Nous allons expliquer schématiquement la notion de convexité (voir ci-après).

Pour trouver arithmétiquement le minimum de la fonction de coût, soit le meilleur couple (a, b), nous allons présenter la méthode numérique de descente de gradient.

C’est une méthode itérative qui se résume ainsi : si vous lâchez un ballon du haut d’une colline, le ballon va prendre à chaque instant la meilleure pente jusqu’en bas de la colline. La convexité de la fonction de coût correspond au fait qu’on est certain, que la colline n’est pas accidentée avec des zones de remontée de pente.

La formulation mathématique de ce problème de descente de gradient s’écrit :

Etape 1 : Initialisation du couple (
Etape 2 : Itération jusqu’à la convergence :

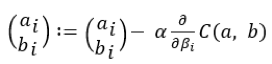
A chaque itération, la meilleure pente est trouvée sur notre fonction C qui se dirige au fil des itérations vers le minimum de la fonction de coût.

Le problème majeur survient dans le cas d’une fonction de coût non convexe. En effet, dans ce cas, il se peut que selon différentes initialisations de la descente du gradient, nous convergions vers un minimum local pour C.

C’est la convexité de la fonction de coût qui permet de lever ce problème puisqu’alors tout minimum local est aussi le minimum global de la fonction (reportez-vous à la figure ci-dessous pour mieux comprendre).

La vitesse de convergence est déterminée par le facteur α devant la dérivée partielle de C dans la formule de descente de gradient ci-dessus. On appelle ce facteur le learning rate et représente la vitesse de modification des paramètres à chaque itération.

– Plus α est grand, plus la modification des paramètres entre deux itérations successives est grande (donc plus la probabilité de « rater » le minimum ou de diverger est grand.

– A l’inverse, plus α est petit, plus nous avons de probabilité de converger vers le minimum (en revanche, le processus de convergence est plus long).

La descente de gradient est l’approche de résolution numérique permettant de trouver une solution au problème de modélisation. Cette méthode permet de trouver, de façon itérative, la meilleure modélisation qui minimise l’erreur en cherchant la meilleure pente jusqu’au minimum global de la fonction de coût.

Cette méthode est particulièrement adaptée aux gros volumes de données et permet d’aboutir le plus rapidement à une solution.

Il existe une autre approche : l’approche analytique.

Dans cette approche, nous résolvons mathématiquement la régression linéaire. Sans rentrer dans les détails mathématiques, il existe une solution analytique au problème par la méthode dite des moindres carrés. Si vous souhaitez en savoir plus, une forme de résolution analytique pour la régression linéaire s’écrit :

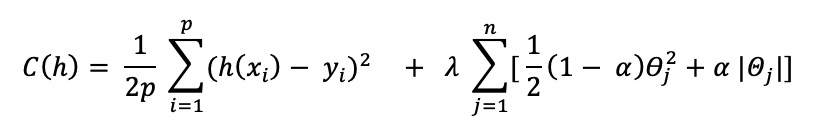
À vous d’approfondir la question si vous le souhaitez.

Et dans la pratique…

Un de points délicats de la mise en œuvre d’un modèle de régression linéaire vient de l’instabilité de la prédiction face à l’intégration de nouvelles observations dans les données (c’est-à-dire que les coefficients de chaque variable explicative peuvent changer fortement pour quelques observations supplémentaires ajoutées à vos données),

Il n’est généralement pas facile de choisir les variables explicatives à prendre en compte en entrée du modèle. Il faut alors se poser des questions sur la nature du processus entre les variables. Quels sont les effets et les causes à intégrer une variable spécifique dans le modèle ? Il faut également trouver une relation immuable entre variables (à l’instar des lois de la physique qui sont universelles et ne changent donc pas, pensez aux lois de l’attraction, de vibration, de transmutation de l’énergie, …),

Dans le cas de la régression linéaire multivariée, une étape supplémentaire de normalisation des variables d’entrée est indispensable. Cette normalisation consiste à transformer toutes les variables en entrée du modèle afin qu’elles évoluent sur une même échelle (c’est pour que l’algorithme de descente de gradient puisse fonctionner correctement),

Le modèle linéaire ne convient pas pour tous les phénomènes physiques en jeu (par exemple : les phénomènes d’échauffement thermique se modélisent généralement grâce à des relations quadratiques entre mesures physiques électriques). Si le phénomène n’est pas modélisable par une relation linéaire entre les variables d’entrée et la cible, il faut alors penser à rechercher une fonction polynomiale. (Mais dans ce cas, attention au sur-apprentissage à savoirle fait d’apprendre des fausses relations dans vos données !),

Retenez les points positifs du modèle linéaire : c’est une approche intéressante parce que le modèle est simple à expliquer aux métiers et le modèle est explicable (les coefficients de chaque variable normalisée donnent une idée de l’importance de la variable dans la relation).

Conclusion :

Nous avons vu que la régression linéaire permet de vous familiariser avec les grands principes de construction d’un modèle de Machine Learning. Dans l’un de nos prochains articles, nous verrons comment améliorer la stabilité des modèles de régression linéaire par pénalisation LASSO, RIDGE ou ELASTICNET.