
L’algorithme des k plus proches voisins, en anglais k-NN pour « k Nearest Neighbors » est un algorithme simple à comprendre.
D’abord, vous devez savoir qu’il s’agit d’un algorithme d’apprentissage supervisé qui permet à la fois de résoudre un problème de classification et de régression.
Pour rappel, on parle d’apprentissage supervisé lorsque qu’un algorithme, pour pouvoir apprendre, a besoin de données d’entrée (c’est-à-dire, des entrées ayant une étiquette) et des données de sortie (c’est-à-dire que l’algorithme va devoir prédire par la suite) labellisées .
L’idée est la suivante : il y a une phase d’apprentissage de l’algorithme qui doit s’entraîner à apprendre la relation entre les entrées et les sorties des données.
C’est un point fondamental. En effet, un apprentissage supervisé repose sur l’organisation des données selon une série de couples {entrées-sorties}.
Et ensuite, une fois l’algorithme entraîné, celui-ci peut prédire une valeur de sortie à partir de ses seules valeurs d’entrées.
Principe de la méthode des k plus proches voisins
Une fois la phase d’apprentissage de l’algorithme réalisée, pour faire une prédiction à partir d’une nouvelle observation inconnue, l’algorithme trouve dans le jeu de données d’apprentissage, l’observation qui lui est la plus proche.
Ensuite, l’algorithme assigne l’étiquette de cette donnée d’apprentissage à la nouvelle observation qui était inconnue.
Le k dans la formule « k plus proches voisins » signifie qu’à la place de se contenter du seul voisin le plus proche de l’observation inconnue, nous pouvons prendre en compte un nombre fixé k de voisins du jeu d’apprentissage.
Enfin, nous pouvons faire une prédiction en nous basant sur la classe majoritaire dans ce voisinage.
Le principe peut paraître compliqué à expliquer mais regardez plutôt l’exemple ci-dessous qui illustre simplement l’idée générale de cette méthode.
Illustrons simplement le principe de fonctionnement de l’algorithme

Figure 1 : L’algorithme du k-NN et son principe de fonctionnement par l’exemple
En résumé, les étapes de l’algorithme sont les suivantes :
A partir des données d’entrée :
- On choisit une fonction de définition pour la distance (on parle aussi de fonction de similarité) entre observations.
(Nous reviendrons sur cette étape dans le paragraphe suivant).
- On fixe une valeur pour k, nombre de plus proches voisins.
Pseudo code :
Pour une nouvelle observation inconnue en entrée dont on veut prédire sa variable de sortie, il faut faire :
- Etape 1 – Calculer toutes les distances entre cette observation en entrée et les autres observations du jeu de données,
- Etape 2 – Conserver les k observations du jeu de données qui sont les plus « proches » de l’observation à prédire,
Nota : pour déterminer si une valeur est plus ou moins « proche » d’une autre, on utilise une fonction de similarité reposant sur un calcul de distance (se reporter au paragraphe suivant).
- Etape 3 – Prendre les valeurs des observations retenues :
- Si on effectue une régression, l’algorithme calcule la moyenne (ou la médiane) des valeurs des observations retenues,
- Si on effectue une classification, l’algorithme assigne le label de la classe majoritaire à la donnée qui était inconnue.
- Etape 4 – Retourner la valeur calculée dans l’étape 3 comme étant la valeur qui a été prédite par l’algorithme pour l’observation en entrée qui était inconnue.
Pour cet algorithme, le choix du nombre k et le choix de la fonction de similarité sont des étapes qui peuvent conduire à une forte variabilité des résultats.
Métriques d’évaluation de la similarité entre les observations
Comme on vient de le dire, pour mesurer la proximité entre les observations, on doit imposer une fonction de similarité à l’algorithme.
Cette fonction qui calcule la distance entre deux observations estime l’affinité entre les observations comme ceci : « Plus deux points sont proches l’un de l’autre, plus ils sont similaires. »
Cependant, cette affirmation triviale s’accompagne de quelques nuances en mathématiques et il existe de nombreuses fonctions de similarité dans la littérature.
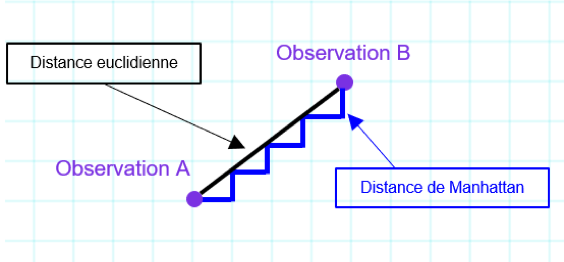
Figure 2 : Distance entre deux points : distance euclidienne versus distance de Manhattan (plusieurs chemins entre A et B)
Parmi les fonctions de similarité les plus connues, il y a la distance euclidienne. C’est cette fonction que nous avons utilisée dans notre exemple plus haut.
Il s’agit de la fonction de similarité la plus intuitive puisqu’elle formalise l’idée de distance : la distance en ligne droite qui sépare deux points dans l’espace.
La distance de Manhattan correspond à un déplacement à un angle droit sur un damier.
Si cela vous intéresse, je vous invite à regarder les définitions mathématiques d’autres métriques telles que la fonction de Minkowski, la fonction de Jaccard, la distance de Hamming, la distance de Levenshtein, la métrique de Jaro ou encore la distance de Jaro-Winker.
Il faut savoir qu’on choisit généralement la fonction de distance en fonction des types de données qu’on manipule et du sens mathématique ou physique du problème qu’on a à résoudre. Très schématiquement, pour les données quantitatives (exemple : la taille, le poids, le salaire, le chiffre d’affaire etc…), la distance euclidienne est un bon choix pour commencer.
La distance de Manhattan peut être intéressante pour des données qui ne sont pas du même type (c’est-à-dire des données qui n’ont pas été misee sur la même échelle).
Aussi, je vous conseille vivement d’approfondir le sujet pour maîtriser les cas d’utilisation classiques de ces différentes fonctions de similarité en fonction des problèmes à résoudre.
A vous de coder … (Python)
Ce paragraphe fournit quelques éléments pour coder l’algorithme vous-même. Tous les modèles de machine learning de scikit-learn sont implémentés dans leurs propres classes, qui sont appelées les classes Estimator (estimateur).
La classe pour l’algorithme des k plus proches voisins est KNeighborsClassifier du module neighbors.
Avant de pouvoir utiliser le modèle, nous devons l’instancier comme suit :

Dans notre exemple, l’objet classifier encapsule l’algorithme qui va être utilisé pour bâtir le modèle à partir des données d’apprentissage tout comme l’algorithme qui permettra de faire des prédictions pour les nouvelles observations.
Pour construire le modèle du k-NN, nous devons d’abord splitter les données en 2 bases : une base de données pour l’apprentissage de l’algorithme et une base de données pour tester la performance obtenue.

Nota : test_size = 0,2 = 20% donne la taille de la base de données de test soit 20% de l’échantillon initial de données.
Ensuite, nous appelons la méthode fit de l’objet classifier, qui prend en arguments le jeu de données d’apprentissage X_train et le jeu de données de test y_train.

La méthode fit retourne l’objet knn elle-même.
La configuration de l’algorithme par défaut est la suivante :
KNeighborsClassifier (algorithm=’auto’, leaf_size=30 , metric=’minkowski’, n_jobs=1, n_neighbors=3, p=2, weights=’uniforms’)
Vous noterez que tous les paramètres ont leur valeur par défaut à l’exception du nombre de plus proches voisins fixé à n_neighbors=3.
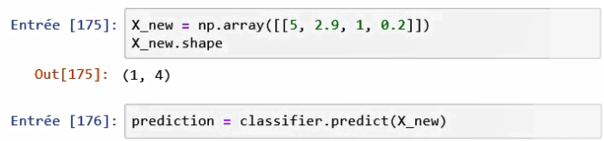
Pour faire une prédiction portant sur de nouvelles données inconnues, nous créons un vecteur qui contient les données d’entrée connues. Ci-dessous, il s’agit du vecteur X_new.
Puis, nous utiliserons la méthode predict de l’objet classifier.
Limites de l’algorithme des k plus proches voisins
Si le fonctionnement de l’algorithme des plus proches voisins est facile à comprendre, le principal inconvénient de la méthode est son coût en termes de complexité. En effet, l’algorithme cherche les k plus proches voisins pour chaque observation. Ainsi, si la base de données est très grande (quelques millions de lignes), le temps de calcul peut devenir extrêmement long. Il faut donc porter une attention particulière à la taille du jeu de données d’entrée.
Autre point d’attention : le choix de fonction de similarités peut conduire à des résultats très différents entre modèles.
Il est donc recommandé de faire un état de l’art rigoureux pour mieux choisir la distance de similarité en fonction du problème à résoudre et surtout il est recommandé de tester plusieurs combinaisons pour estimer l’impact sur les résultats.
Retenez malgré tout que si l’algorithme des k-NN est intéressant du point de vue didactique, il n’est presque jamais utilisé tel quel par les data-scientists.
Conclusion
Si vous souhaitez apprendre à coder vous-même un algorithme des k plus proches voisins à partir d’une base de données réelle, je vous invite à suivre notre webinar « Comment construire une segmentation marketing efficace ? (Partie 2) ». Cette formation vous permettra d’avoir un aperçu des principales techniques de machine learning pour réaliser une segmentation marketing.
Nous y présentons les principaux algorithmes de machine learning qui permettent de faire de la segmentation comme l’algorithme du k plus proches voisins par exemple. Mais, nous présentons également les algorithmes bien connus du K-Means, de la classification hiérarchique ascendante (CAH) et nous revenons également sur les approches métiers historiques de segmentation telles que la méthode RFM (Récence, Fréquence, Montant) par exemple.