Learning by doing : l’apprentissage par renforcement

Nous prenons au quotidien de nombreuses décisions en fonction de nos expériences passées, de l’avis des autres ou encore du rapport bénéfice/risque que comporte notre choix sur le court-terme comme sur le long-terme.

Une branche du Machine Learning (ML) fonctionne de la même manière : il s’agit de l’apprentissage par renforcement, dit Reinforcement Learning (RL) en anglais.

Cette discipline est utilisée pour résoudre des problématiques de prise de décisions séquentielles, dans le but de maximiser les gains d’une séquence d’opérations, selon des objectifs spécifiques.

 

Apprentissage par renforcement

L’apprentissage par renforcement (RL) est un domaine du Machine Learning, au même titre que l’apprentissage supervisé ou non supervisé. Son objectif est de créer des agents capables de prendre les meilleures décisions possibles.

Le RL se base donc sur un système de récompenses : à chaque action effectuée, l’agent reçoit une récompense (ou une pénalité dans le cas où l’action est mal réalisée) de la part de l’environnement, qui va lui permettre d’ajuster sa stratégie.

L’agent apprend donc à agir de façon à maximiser les récompenses espérées sur le long terme.

Fig. 1: Scénario typique de RL (Source : Wikipédia)

 

Prenons un exemple simple pour mieux comprendre les grands principes du RL.

La startup britannique Wayve a réussi à concevoir une voiture autonome capable de suivre une ligne droite en une journée grâce au RL. Dans cet exemple :

• l’agent est le logiciel qui conduit la voiture,
• l’environnement est l’espace virtuel dans lequel le véhicule évolue,
• l’action à un instant t, c’est la possibilité de changer de direction, de ralentir, d’accélérer etc…,
• la récompense est associée dans le cas où le véhicule circule correctement dans son environnement (à défaut, une pénalité est associée si le véhicule se heurte à un obstacle, par exemple),
• On parle de politique pour désigner le mécanisme qui lie les récompenses observées dans le passé et l’état du système à l’instant t.

 

La robotique n’est pas le seul domaine qui a bénéficié de l’avancée du RL.

 

Voici quelques cas d’usage :

 

• Le logiciel AlphaGo de la société Deep Mind a battu en 2016 Lee Sedol, multiple champion du monde du jeu de Go, 

• “Five” d’openIA : cet agent logiciel sur-entraîné à jouer au jeu vidéo Dota 2 a réussi à battre toute une équipe de joueurs professionnels,

• Le Stanford Neuromuscular Biomechanics a réussi à concevoir des prothèses de jambes nouvelle génération, capables d’apprendre la façon de marcher de leurs utilisateurs afin de leur rendre le mouvement plus facile. Leur approche a consisté à entraîner à la course une maquette numérique de corps humain par RL,

• Recommandation de produits : Les préférences des utilisateurs sont amenées à changer fréquemment. Voilà pourquoi recommander des produits aux utilisateurs en fonction de leur comportement passé pourrait rapidement devenir obsolète. L’apprentissage par renforcement permet d’améliorer sensiblement les modèles classiques de recommandation de produits, 

• Ingénierie : Facebook a développé une plateforme de RL open source en vue d’améliorer les notifications pour leurs utilisateurs, d’optimiser la qualité des flux vidéos et d’optimiser la production et mise à l’échelle de leur application.

 

Le RL est également présent dans de nombreux autres domaines : le NLP (Natural Language Processing), la santé, la programmation génétique ou encore le retail. Les champs d’application sont très vastes.

 

Learning by doing : l’exemple Cart-Pole d’OpenIA

 

Le problème du pendule inversé ou “cart-pole problem” décrit un chariot qui se déplace à gauche ou à droite sur un axe x. Une tige est fixée par un pivot à ce chariot et le but de l’agent est de maintenir à une position d’équilibre (la position verticale) la tige du chariot. L’agent doit déplacer le chariot vers la gauche ou la droite pour maintenir la tige en position verticale, position d’équilibre très instable !

Il est possible de simuler ce problème du cart-pole par un environnement virtuel disponible dans la librairie Gym sur Python développée par OpenIA.

 

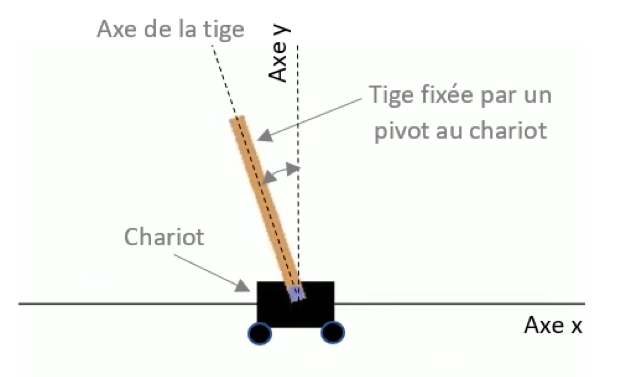
Fig. 2 : Problème du pendule inversé ou “cart-pole problem”

 

Chaque observation est un vecteur composé de 4 valeurs :

• la position du chariot sur l’axe x,
• la vitesse du chariot sur l’axe x,
• l’angle entre l’axe de la tige et l’axe y (0 = vertical),
• la vitesse angulaire de la tige (vitesse de rotation de la tige autour de son pivot).

 

L’agent peut alors choisir une action en fonction de l’observation à chaque itération. Les observations possibles sont :

• déplacer le chariot à gauche : action “0”,
• déplacer le chariot à droite : action “1”.

 Une variable appelée variable “done” nous indique l’état de la tige à chaque itération :

• done prend la valeur “Faux” si la tige est toujours en position verticale (position d’équilibre),
• done prend la valeur “Vrai” si la tige bascule à gauche ou à droite.

 

Le but de l’agent est de maintenir la tige à sa position d’équilibre le plus longtemps possible. Lorsque l’action de l’agent permet de maintenir l’équilibre de la tige, l’agent se voit alors attribuer une récompense de +1. Le jeu s’arrête quand la tige tombe et qu’il n’est plus possible d’espérer un retour à la position d’équilibre.

 

Nous allons choisir 2 politiques avec des niveaux de complexité différents. Une politique correspond à une séquence, une stratégie d’actions réalisées par l’agent (mouvement du chariot à gauche ou à droite).

Puis, nous allons analyser les résultats afin de voir laquelle des politiques est la plus fructueuse.

Pour chaque politique, nous allons effectuer 500 simulations dans le but d’avoir une estimation précise et statistiquement significative des récompenses.

 

Politique aléatoire

Cette politique consiste à choisir une action au hasard : aller à gauche = 0 ou aller à droite = 1, indépendamment de l’observation courante (la position courante de la tige).

 

Voyez plutôt la routine, ci-dessous, codée en python :

 

totals = [] # pour chaque simulation for episode in range(500):    # réinitialiser récompense    episode_rewards = 0    # réinitialiser environnement    obs = env.reset()    while True:        # choix aléatoire de l’action entre 0 (gauche) et 1 (droite)        obs, reward, done, info = env.step(np.random.randint(0,2))        # stocker récompense        episode_rewards += reward        # arrêter si le poteau tombe        if done:            break    totals.append(episode_rewards)

 

Nous voyons que chaque simulation s’arrête quand la variable « done » est vraie. Nous nous attendons à ce que cette politique qui repose sur le hasard conduise à un nombre de récompenses faibles.

 

Politique basique : 

Cette politique fonctionne d’une manière un peu plus logique.

L’action est définie en fonction de l’angle de la tige : si la tige est penchée à gauche (angle négatif), alors nous déplaçons le chariot vers la gauche pour espérer revenir à la position d’équilibre. A contrario, si la tige est penchée à droite, alors nous déplaçons le chariot à droite pour espérer revenir à l’équilibre.

 

totals = [] # pour chaque simulation for episode in range(500):    # réinitialiser récompense    episode_rewards = 0    # réinitialiser environnement    obs = env.reset()    while True:        # choix de l’action en fonction de l’angle        position, velocity, angle, angular_velocity = obs        if angle < 0:            action = 0        else:            action = 1        obs, reward, done, info = env.step(action)        # arrêter si le poteau tombe        episode_rewards += reward        if done:            break    totals.append(episode_rewards)

  

Comparaison des résultats pour chacune des deux politiques

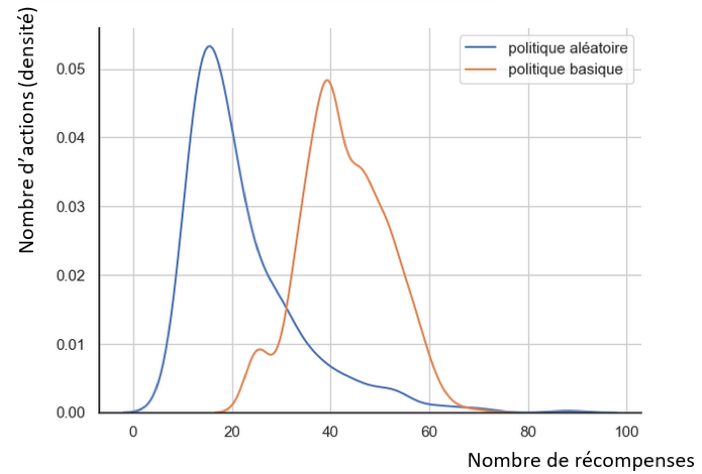
Fig. 3 : Distributions des récompenses pour chaque politique

 

Statistiquement, la politique basique est la meilleure des deux politiques. En effet, en moyenne deux fois plus de récompenses sont attribuées en politique basique par rapport à un fonctionnement en politique aléatoire.

 

Autres solutions plus avancées :

Il existe d’autres solutions beaucoup plus élaborées avec notamment l’utilisation de réseaux de neurones. Ces modèles neuronaux se basent sur les gradients de politique, c’est-à-dire une fonction mathématique modélisant l’erreur passée.

Les réseaux de neurones prennent ainsi des décisions plus complexes en considérant l’état passé du système (actions précédentes et leurs conséquences).

Si une action est bonne, elle augmente le gradient de politique, et inversement si elle est mauvaise, elle le réduit.

Mais comment savoir si une action est bonne ou mauvaise ? En effet, la plupart des actions ont des effets retardés. Par exemple, lorsque vous gagnez ou perdez des points dans un jeu, il n’est pas systématiquement possible de savoir quelle est l’action qui a contribué à ce résultat. Est-ce seulement la dernière action? ou bien est-ce la succession des dix dernières actions ? …

L’algorithme des gradients politiques s’attaque à ce problème. En effet, la succession de tous les états passés du système est modélisée et gardée en mémoire.

Ce genre de politique surpasse largement les politiques basiques (cf. exemple du paragraphe précédent) par une complexité introduite dans la prise de décision, basée sur la mémoire du système.

 

Conclusion

Dans ce bref article, nous avons vu les grands principes du fonctionnement de l’apprentissage par renforcement.

Il s’agit d’un domaine du Machine Learning qui est porteur de beaucoup de promesses. Et, dans le cadre d’un cas d’usage autour de la recommandation de produits, nous avons eu l’occasion de mesurer la performance de ce type d’approches par rapport à une approche “classique” de Machine Learning.

 

Dans un prochain article, nous vous proposerons d’approfondir le sujet et vous apprendrez ce qu’est un algorithme UCB, LUCB. Nous vous proposerons d’étudier une architecture Google Cloud Plateform pour mettre en perspective les principes du RL.